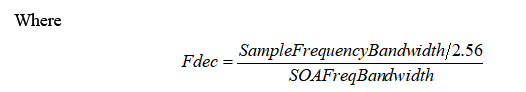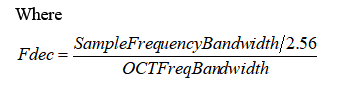NVGate DSP computation SPU
Force DSP
On force DSP (and normal DSP), the number of SPU change according to the max sampling frequency. The more you have data to analyse (high sampling frequency), the less you have power computation (SPU). We have:
| Sampling Frequency (kHz) | Number of SPU / DSP (Normal or Force) |
|---|---|
| 102.4 | 6 |
| 65.536 | 9 |
| 51.2 | 12 |
| 32.768 | 18 |
| 25.6 | 24 |
| 16.384 | 36 |
| 12.8 | 48 |
| 6.4 | 96 |
| 3.2 | 192 |
| 1.6 | 384 |
FFT
According to the architecture of force DSP, the SPU computation per channels is not linear. So we have the following table for real time SPU computation :
| Number of FFT lines | Normal DSP: SPU / channel | Force DSP: SPU / channel |
|---|---|---|
| 401 | 1 | 0.33 |
| 801 | 1.25 | 0.18 (yes !) |
| 1601 | 1.5 | 0.75 |
| 3201 | 2 | 0.8 |
| 6401 | 3 | 2 |
| 12801 | 4 | 2 |
| 25601 | 6 | 3.5 |
Envelope: 401 lines : 2 SPU per channel on force DSP
Zoom: 401 Lines : 0.66 SPU per channel on force DSP.
Recorder
| Recorder Sampling frequency (Hz) | Normal DSP: SPU / channel | Force DSP: SPU / channel |
|---|---|---|
| 51200 or upper | 1 | 0.66 |
| 32768 | 0.66 | 0.44 |
| 25600 | 0.5 | 0.33 |
| 16384 | 0.33 | 0.22 |
| 12800 | 0.25 | 0.167 |
| Else | 0.125 | 0.083 |
Octave
| Octave | Normal DSP: SPU / channel | Force DSP: SPU / channel |
|---|---|---|
| 1/3 | 3 | 1 |
| 1/12 | 6 | 2 |
| 1/24 | 12 | 4 |
OVA
| Normal DSP: SPU / channel | Force DSP: SPU / channel |
|---|---|
| 1 | 0.25 |
TDA
| Normal DSP: SPU / channel | Force DSP: SPU / channel |
|---|---|
| 1 | 0.5 |
SOA
SPU computation for SOA is more complex because it depends of maximum speed, resolution and frequency. Also force DSP computation is not linear.
Force DSP will improve the SPU computation by reducing between 2.5 and 5 to compare with normal DSP.
(@20kHz - 401 lines, we need a maximum of 3 SPUs with normal DSP)
Normal DSP
SPU computation for normal DSP : OR34 V1 - Or35V1 - OR36V1 OR36V22 (normal DSP) - OR38V1 - OR38V2 (Normal DSP).
Because of the computation linearity, we simplify by saying: 1DSP = 12 SPU (no matter the sampling frequency). This allow a simplification for SPU computation. So we can deduce:
FFT
Computation SPUs:
| Bandwidth | Fdec | Resolution | Envelope | Zoom | SPU/Channel for Real-time |
SPU/Channel for non Real-time |
| 20k | 1 | 401 | No | No | 1 | 0,5 |
| 10k | 1 | 401 | No | No | 0,5 | 0,25 |
| Nk | 1 | 401 | No | No | =N/20 | =N/40 |
| 10k | 2 | 401 | No | No | 1 | 1 |
| 5k | 4 | 401 | No | No | 0,8 | 0,6 |
| 2k | 10 | 401 | No | No | 0,6 | 0,6 |
| 1k | 20 | 401 | No | No | 0,5 | 0,6 |
| Lower than 1k |
Higher than 20 |
401 | No | No | 0,5 | 0,5 |
| 20k | 1 | 401 and below |
No | No | 1 | 0,5 |
| 20k | 1 | 801 | No | No | 1,25 | 0,5 |
| 20k | 1 | 1601 | No | No | 1,5 | 0,5 |
| 20k | 1 | 3201 | No | No | 2 | 0,5 |
| 20k | 1 | 6401 | No | No | 3 | 0,5 |
| 20k | 1 | 401 | No | No | 1 | 0,5 |
| 20k | 1 | 401 | No | Yes | 2 | 1,5 |
| 20k | 1 | 401 | No | No | 1 | 0,5 |
| 20k | 1 | 401 | Yes | Yes | 3 | 3 |
SOA
Computation SPUs:
| Bandwidth (Hz) | Decimation factor | Resolution | SPU/Channel |
| 20 k | 1 | 401 | 3 |
| 10 k | 1 | 401 | 1,5 |
| N k | 1 | 401 | =(N*3)/20 |
| 10 k | 2 | 401 | 2 |
| 5 k | 4 | 401 | 1,3 |
| 2,5 k | 8 | 401 | 1,1 |
| 1,25 k | 16 | 401 | 0,9 |
| 625 | 32 | 401 | 0,8 |
| 313 | 64 | 401 | 0,7 |
| 156 | 128 | 401 | 0,6 |
| 78 | 256 | 401 | 0,6 |
| 20 k | 1 | 401 and below | 3 |
| 20 k | 1 | 801 | 3,25 |
Sampling Frequency: set in Front-End/Inputs settings/Input sampling
FFT Bandwidth: set in FFTx/FFT analysis/range
==
Octave:
| Bandwidth | Fdec | Reso | SPU/Channel for Real-time |
| 25.6k | 1 | 1/3rd | 4 |
| 20k | 1 | 1/3rd | 3 |
| 12.8k | 1 | 1/3rd | 2 |
| 10k | 1 | 1/3rd | 1,5 |
| 20k | 1 | 1/3rd | 3,0 |
| 10k | 2 | 1/3rd | 2,0 |
| 5k | 4 | 1/3rd | 1,25 |
| 20k | 1 | 1/1 | 1,5 |
| 20k | 1 | 1/3rd | 3 |
| 20k | 1 | 1/12th | 6 |
| 20k | 1 | 1/24th | 12 |
Sampling Frequency: set in Front-End/Inputs settings/Input sampling
1/N Oct Bandwidth: set in OCT/FFT analysis/range
OVA
| Bandwidth | SPU/Channel for Real-time |
| 25,6k | 1,25 |
| 20k | 1 |
| 12,8k | 0,75 |
| 10k | 0,5 |
The overall acoustic levels analysis requires 1 SPU per channel at 20 kHz bandwidth. The number of required SPUs is directly proportional to the analysis bandwidth (i.e. the sampling frequency divided by 2.56).