NVGate Torsional

Torsional

NVGate propos a comprehensive suite for torsional measurements and analyses.It addresses most of the torsional, cyclic and rotational resonances issues. For both R&D and diagnostics, the latest torsional feature the OROS analyzer the solution for transmissions, engines and electric machinery vibration analysis.

Angular sampling for SOA analysis

The major improvement comes as a simple setting… with large effects. Indeed the possibility to sample the measured signal with a distributed angle pulses of a rotating shaft provides accurate results.

This applies mainly on machineries which feature cyclic variation of their rotating speed. Main ones are:

• Engines (Diesel, Gas, 2/4 strokes)
• Reciprocating pumps or compressors
• Transmission (Torque damper, belt, shaft)
• Electric machines (generator, alternator, motor)

The angular sampling allows getting the exact angle (or phase) of the events in the machine cycle. The results are event better using the time domain averaging (i.e. angular).

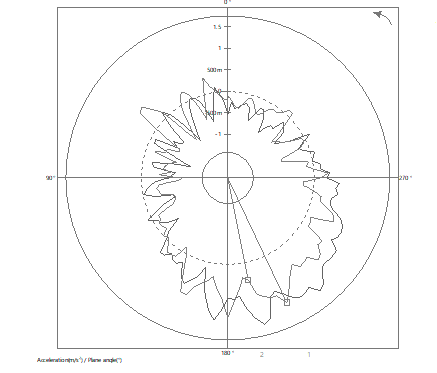
The following example shows the differences between a usual synchronous order analysis and the same one based on angular sampling. The phase differences are clearly visible especially on the ShaftView graphs.

With and without angular sampling Shaft view on an electric machinery bearing

Operations

In order to use the angular sampling function (Optional) it is necessary to have at least:

• A pulses train signal with a known number of pulses/rev
• phase reference (usually a 1 pulse/rev signal)

The sampling signal comes from an ext. synch input. The mode must be set to Sampling or any of the Sampling + xxx

It is necessary to associate a phase reference (the 0°) to the sampling pulse. It can be any tachometer or the sampling input itself. In this last case the 0° will be the first detected pulse or the missing pulse if there are some.

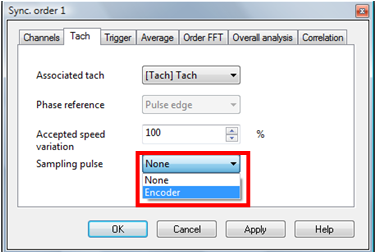
Then the Tachometer and the Sampling are assigned to a SOA plug-in.

The Sampling pulse setting defines if the angular sampling is activated or not:

• If set to None, the SOA will works on the regular way: Interpolation of the sampling dates from the RPM information).
• If set to a sampling input, the SOA will use it for sampling the channels signals

Advantages of the OROS solution

The angular sampling is an old technique which used to be achieved by replacing the sampling clock by an encoder signal. Even if this procedure provides correct order and angles measurement it has a lot of defects. The technique provided by NVGate V8.00 corrects these defects.

The following table compares the possible signal alteration and the OROS solution

Traditional angular sampling	OROS angular sampling
Results are not alias free. It is not possible to apply anti aliasing as the sampling frequency is not known by the acquisition system.	Alias free results. The results are not affected by the alias frequencies thanks to the re-sampling technique. Indeed the analyzer acquires the sample at high freq. (102.4 kS/s) and then re-samples it with a tracking anti-aliasing filter.
The number of pulses/rev. must be a power of 2. Because the digital Fourier transform need a power of 2 samples, if you need to analyze it in order domain (n Revolutions) it is compulsory to deliver n² samples per revolution.	Any number of pulse/rev and any angular resolution are possible. The re-sampling technique used by the SOA allows interpolating the correct number of pulse (n²) from any acquire number of pulses
Missing pulses are not supported. Obviously the missing pulses will conduct to missing samples.	Missing pulses are supported. The OROS torsional measurement is able to interpolate and create the missing pulses. Then the complete pulse sequence is used by the re-sampling algorithm.

NVGate V8.00 allows achieving angular sampled analysis avoiding the artifacts introduced by the direct angular sampling.

Twist measurements (static and dynamic)

Completing the OROS analyzer torsional functions, the twist measurement has been improved and the measurement setup simplified.

The twist measurement consists of computing the angle between the 2 side of transmission shaft (or belt/chain). The measured angle is directly proportional to the stress and the applied torque.

The twist can be:

• Static twist: measure the transmitted torque and power. This is a parameter not for analysis
• Dynamic twist: measure the oscillating stress and resonances. This is a dynamic signal to be analyzed.

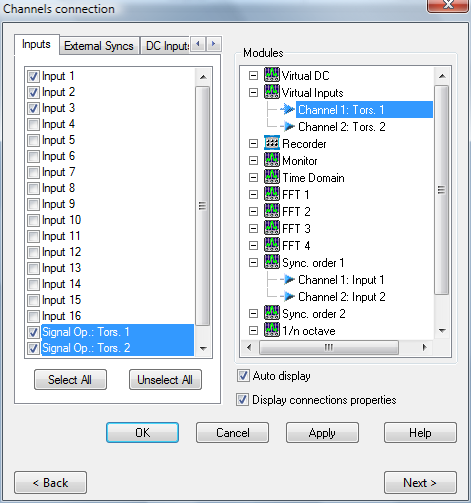
Both signals are computed simultaneously by the virtual input module.

When the torsional signals are settled up, simply connect it to the Virtual input plug-in

For computing the phase between the 2 sides of the twist it is necessary having a tachometer.

This tachometer can come from any of the inputs or directly from one of the torsional signals using the Torsional + tach. mode.

Then click on the Tools/Virtual inputs/dynamic button to open the virtual inputs setting. Click on the Twist tab. Select each torsional signal from the source 1 and source 2 lists.

The twist will be displayed in angle or torque. The coefficient is used to convert the read angle in torque.

The result are available from the add/Remove windows under the virtual input tab.

Uncorrelated pulse number

Note that the any number of pulses/rev can be used for twist computation and these numbers of pulses/rev can either be different on each side.

The following table describes the difference between classical twist measurement and the OROS one:

Classical twist measurement	OROS twist
Twist measurement force having the same number of pulse on each side. The difference between the 2 signals is requiring the same number of sample/rev.	Twist support different number of pulse/rev signals. The OROS twist algorithm is based on phase computation rather than pulse timing comparison. Thanks to this the analysis is independent from the number of pulses/rev.
Twist measurement based on integration of the angular speed (torsional) is not stable	Twist signal is stable and do not diverge. Indeed the OROS Twist algorithm do not uses integration techniques

Fractional missing pulses management

The missing pulses are a common situation faced while doing torsional measurement. In the case of a classical flywheel (60:2) it is easy to set and measure excluding this 2 missing pulses. But most of the measurement done on the industry do not offer the comfort of an encoder or gear teeth access.

A very useful solution is the piano (or zebra) tape which is glued on the shaft and read by an optical probe: Easy to install and to use.

But the main problem is to have an entire number of pulses. This is never achievable because the various parameters are difficult to control: Black/white period, diameter of the shaft, thickness of the tape/glue. Well, don't try, this is not possible.

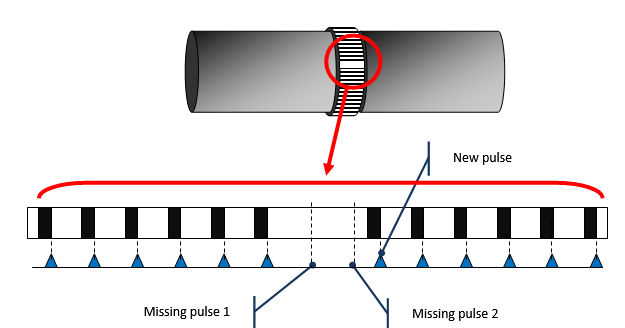
The solution is to leave a hole which is interpreted as missing pulse. Due to the above variables it will be a fractional number of missing pulse.

OROS torsional function is able to manage such fractional pulses. It offers to achieve torsional measurement on the field in a simple and easy way.

Piano tape junction for fractional missing pulse management

The empty area (missing teeth) length at the piano tape junction must be included between 1 and 3 teeth. The number of missing teeth must be set to the exact number of missing teeth: In this example: 2.

Note: the total number of teeth includes the missing teeth.