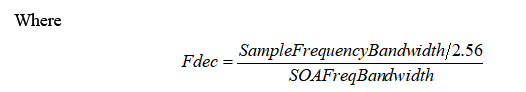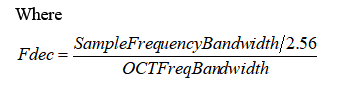Difference between revisions of "NVGate DSP computation SPU"
(→SOA) |
(→SOA) |
||
| Line 109: | Line 109: | ||
SPU computation for SOA is more complex because it depends of maximum speed, resolution and frequency. Also force DSP computation is not linear. | SPU computation for SOA is more complex because it depends of maximum speed, resolution and frequency. Also force DSP computation is not linear. | ||
@ | @20kHz bandwith , 401 lines: we need a maximum of 3 SPU with normal DSP. | ||
Force DSP will improve this by divided beetween 2.5 and 5 the SPU computation. | Force DSP will improve this by divided beetween 2.5 and 5 the SPU computation. | ||
Revision as of 16:41, 15 February 2022
Force DSP
On force DSP (and also for normal DSP...), the number of SPU change according to the max sampling frequency. We have:
| Sampling Frequency in kHz | Number of SPU / DSP (Normal or Force) |
|---|---|
| 102.4 | 6 |
| 65.536 | 9 |
| 51.2 | 12 |
| 32.768 | 18 |
| 25.6 | 24 |
| 16.384 | 36 |
| 12.8 | 48 |
| 6.4 | 96 |
| 3.2 | 192 |
| 1.6 | 384 |
FFT
According to the architecture of force DSP, the SPU computation per channels is not linear. So we have the following table for real time SPU computation :
| Number of FFT lines | Normal DSP: SPU / channel | Force DSP: SPU / channel |
|---|---|---|
| 401 | 1 | 0.33 |
| 801 | 1.25 | 0.18 |
| 1601 | 1.5 | 0.75 |
| 3201 | 2 | 0.8 |
| 6401 | 3 | 2 |
| 12801 | 4 | 2 |
| 25601 | 6 | 3.5 |
Envelope: 51.2kHz - 401 lines : 2 SPU per channel on force DSP
Zoom: 51.2kHz - 401 Lines : 0.66 SPU per channel on force DSP.
Recorder
| Recorder Sampling frequency (Hz) | Normal DSP: SPU / channel | Force DSP: SPU / channel |
|---|---|---|
| 51200 or upper | 1 | 0.66 |
| 32768 | 0.66 | 0.5 |
| 25600 | 0.5 | 0.33 |
| 16384 | 0.33 | 0.25 |
| 12800 | 0.25 | 0.125 |
| Else | 0.125 | 0.075 |
Octave
| Octave | Normal DSP: SPU / channel | Force DSP: SPU / channel |
|---|---|---|
| 1/3 | 1 | 0.33 |
| 1/12 | 2 | 0.66 |
| 1/24 | 4 | 1.33 |
OVA
| Normal DSP: SPU / channel | Force DSP: SPU / channel |
|---|---|
| 1 | 0.25 |
TDA
| Normal DSP: SPU / channel | Force DSP: SPU / channel |
|---|---|
| 1 | 0.5 |
SOA
SPU computation for SOA is more complex because it depends of maximum speed, resolution and frequency. Also force DSP computation is not linear.
@20kHz bandwith , 401 lines: we need a maximum of 3 SPU with normal DSP. Force DSP will improve this by divided beetween 2.5 and 5 the SPU computation.
Normal DSP
SPU computation for normal DSP : OR34 V1 - Or35V1 - OR36V1 OR36V22 (normal DSP) - OR38V1 - OR38V2 (Normal DSP).
Because of the linearity of the computation, we simplify by saying: 1DSP = 12 SPU (no matter the sampling frequency). This allow a simplification for SPU computation. So we can deduce:
FFT
Computation SPUs:
| Bandwidth | Fdec | Resolution | Envelope | Zoom | SPU/Channel for Real-time |
SPU/Channel for non Real-time |
| 20k | 1 | 401 | No | No | 1 | 0,5 |
| 10k | 1 | 401 | No | No | 0,5 | 0,25 |
| Nk | 1 | 401 | No | No | =N/20 | =N/40 |
| 10k | 2 | 401 | No | No | 1 | 1 |
| 5k | 4 | 401 | No | No | 0,8 | 0,6 |
| 2k | 10 | 401 | No | No | 0,6 | 0,6 |
| 1k | 20 | 401 | No | No | 0,5 | 0,6 |
| Lower than 1k |
Higher than 20 |
401 | No | No | 0,5 | 0,5 |
| 20k | 1 | 401 and below |
No | No | 1 | 0,5 |
| 20k | 1 | 801 | No | No | 1,25 | 0,5 |
| 20k | 1 | 1601 | No | No | 1,5 | 0,5 |
| 20k | 1 | 3201 | No | No | 2 | 0,5 |
| 20k | 1 | 6401 | No | No | 3 | 0,5 |
| 20k | 1 | 401 | No | No | 1 | 0,5 |
| 20k | 1 | 401 | No | Yes | 2 | 1,5 |
| 20k | 1 | 401 | No | No | 1 | 0,5 |
| 20k | 1 | 401 | Yes | Yes | 3 | 3 |
SOA
Computation SPUs:
| Bandwidth (Hz) | Decimation factor | Resolution | SPU/Channel |
| 20 k | 1 | 401 | 3 |
| 10 k | 1 | 401 | 1,5 |
| N k | 1 | 401 | =(N*3)/20 |
| 10 k | 2 | 401 | 2 |
| 5 k | 4 | 401 | 1,3 |
| 2,5 k | 8 | 401 | 1,1 |
| 1,25 k | 16 | 401 | 0,9 |
| 625 | 32 | 401 | 0,8 |
| 313 | 64 | 401 | 0,7 |
| 156 | 128 | 401 | 0,6 |
| 78 | 256 | 401 | 0,6 |
| 20 k | 1 | 401 and below | 3 |
| 20 k | 1 | 801 | 3,25 |
Sampling Frequency: set in Front-End/Inputs settings/Input sampling
FFT Bandwidth: set in FFTx/FFT analysis/range
==
Octave:
| Bandwidth | Fdec | Reso | SPU/Channel for Real-time |
| 25.6k | 1 | 1/3rd | 4 |
| 20k | 1 | 1/3rd | 3 |
| 12.8k | 1 | 1/3rd | 2 |
| 10k | 1 | 1/3rd | 1,5 |
| 20k | 1 | 1/3rd | 3,0 |
| 10k | 2 | 1/3rd | 2,0 |
| 5k | 4 | 1/3rd | 1,25 |
| 20k | 1 | 1/1 | 1,5 |
| 20k | 1 | 1/3rd | 3 |
| 20k | 1 | 1/12th | 6 |
| 20k | 1 | 1/24th | 12 |
Sampling Frequency: set in Front-End/Inputs settings/Input sampling
1/N Oct Bandwidth: set in OCT/FFT analysis/range
OVA
| Bandwidth | SPU/Channel for Real-time |
| 25,6k | 1,25 |
| 20k | 1 |
| 12,8k | 0,75 |
| 10k | 0,5 |
The overall acoustic levels analysis requires 1 SPU per channel at 20 kHz bandwidth. The number of required SPUs is directly proportional to the analysis bandwidth (i.e. the sampling frequency divided by 2.56).