Difference between revisions of "NVGate CBT principle and settings"
| (6 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
Constant Band Tracking feature consists | [[category:WikiOros]] | ||
Constant Band Tracking (CBT) feature consists of Order analysis calculations based on energy summation from FFT data. Summation bands (in Hz) defined by a user will be fixed over time, through run up or down condition of the measurement. The provided tach signal is connected to FFT and energy summation around multiple (integer or not) of rotating frequency will be calculated in real-time. | |||
FFT | For FFT Spectrums giving discrete frequency lines, energy summation will be based on the summation of spectral lines values. The minimum number of lines to be taken into account is related to windowing function used for time block filtering. Up to 8 different orders may be extracted per channels. Order selection may be different from one channel to another. | ||
=== Setting Constant Band | === Setting Constant Band Tracking Parameters=== | ||
=====a/ Order | =====a/ Order Amplitude Extraction===== | ||
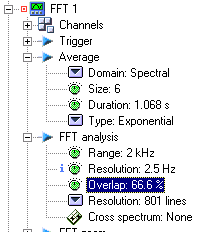
Order amplitude extraction from FFT spectra is highly | Order amplitude extraction from FFT spectra is highly dependent on FFT speed itself. High resolution in FFT setting (very small delta f) will result in long trigger blocks and consequently slow FFT refreshes. Fast run or run down conditions (quickly changing vibration signature) may therefore be incompatible with slow FFT calculations. One way to avoid this problem may be to reduce Spectrum resolution to an acceptable value and add an Overlap (see picture 1) in FFT calculation. | ||
The number of averages is also a parameter to look after as too many averages may smooth run up/down vibration signature. Contrarily too few averages may result in a noisy looking order amplitude curve. | |||
[[Image:CBT_01.png|framed|none]] | [[Image:CBT_01.png|framed|none]] | ||
| Line 15: | Line 16: | ||
=====b/ Frequency bandwidth definition===== | =====b/ Frequency bandwidth definition===== | ||
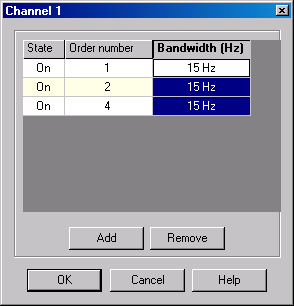
Frequency band on which order amplitude may be extracted is to be defined by user for each channel (see picture 2). Too wide frequency band definition may lead to measurement | Frequency band on which order amplitude may be extracted is to be defined by user for each channel (see picture 2). Too wide of a frequency band definition may lead to measurement errors, as harmonics from rotation speed may be very close at low speed. For instance at 1000 RPM, Order 1 will be at 16.6Hz, Order 2 at 33.2Hz, defining a frequency band for energy summation of 50Hz for instance for order 1 will result in integrating Order 1 and Order 2 in this case. More generally speaking the amplitude value of Order 1 calculated with Constant Band Tracking technique may often be overestimated during low speed analysis process. | ||
[[Image:CBT_02.png|framed|none]] | [[Image:CBT_02.png|framed|none]] | ||
| Line 25: | Line 26: | ||
Minimum band available is directly related to weighting window type used in FFT calculation. | Minimum band available is directly related to weighting window type used in FFT calculation. | ||
Due to window shape, energy of a pure tone sine wave for instance may be split on 3 | Due to window shape, energy of a pure tone sine wave for instance may be split on 3 or more spectral lines. Consequently, a minimum frequency band will be proposed in the setting window. | ||
Example of Hanning window: | Example of Hanning window: | ||
From the curve shown in Picture 3, | From the curve shown in Picture 3, you can see that applying Hanning weighting window on a pure tone sine wave will result in energy spread between the 2 side spectral lines (-1 and <nowiki>+</nowiki>1 on Picture 3) of sine frequency. Energy on the next spectral lines (-2 and <nowiki>+</nowiki>2 on Picture 3) will be reduced to 0 amplitude. | ||
Picture 3: Hanning weighting window | Picture 3: Hanning weighting window | ||
[[Image:cbt formula.png|framed|none]] | |||
| | |||
| | |||
=====c/ Phase calculation in Constant Band Tracking===== | =====c/ Phase calculation in Constant Band Tracking===== | ||
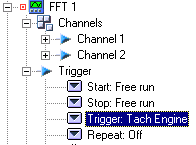
In order to extract precise phase information from Constant Band Tracking, measurement | In order to extract precise phase information from Constant Band Tracking, measurement have to be synchronized with rotational speed. Acquisitions of FFT blocks (trigger block) will need to be synchronized with Tach pulses in order to guaranty exact start condition in time (see Picture 4). | ||
[[Image:CBT_04.png|framed|none]] | [[Image:CBT_04.png|framed|none]] | ||
| Line 64: | Line 47: | ||
''Increase of phase precision with averaging domain.'' | ''Increase of phase precision with averaging domain.'' | ||
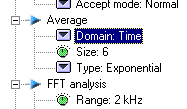
Provided the FFT trigger condition is set to Tach pulses, averaging domain be can be set to Time. This will | Provided the FFT trigger condition is set to Tach pulses, averaging domain be can be set to Time. This will activate Time Shift Resampling (see User Note: S015-081-1 Time shift resampling) in time domain and therefore increasing phase accuracy of trigger block by a factor of 16.(see Picture 5) | ||
[[Image:CBT_05.png|framed|none]] | [[Image:CBT_05.png|framed|none]] | ||
| Line 70: | Line 53: | ||
Picture 5: Time domain averaging setting | Picture 5: Time domain averaging setting | ||
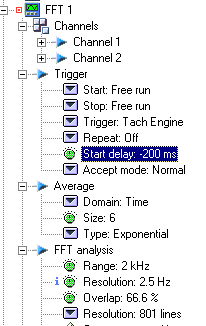
Similarly, to guaranty that core information of Trigger | Similarly, to guaranty that core information of Trigger Blocks (and therefore phase information) are not filtered out by weighting window, it is recommended to center time Trigger Blocks by shifting them half a block. This is made possible through the 'Start Delay' feature by adjusting it to a negative value of half the size of a trigger block (equivalent to 1/<nowiki>[</nowiki>2*"delta"f<nowiki>]</nowiki>, where "delat"f is the spectral resolution). (see picture 6) | ||
[[Image:CBT_06.png|framed|none]] | [[Image:CBT_06.png|framed|none]] | ||
Picture 6: Trigger delay setting in CBT | Picture 6: Trigger delay setting in CBT | ||
=== Difference beetween CBT and SOA === | |||
[[NVGate_SOA_and_CBT_techniques#Principles|Read this page.]] | |||
Latest revision as of 09:58, 26 November 2024
Constant Band Tracking (CBT) feature consists of Order analysis calculations based on energy summation from FFT data. Summation bands (in Hz) defined by a user will be fixed over time, through run up or down condition of the measurement. The provided tach signal is connected to FFT and energy summation around multiple (integer or not) of rotating frequency will be calculated in real-time.
For FFT Spectrums giving discrete frequency lines, energy summation will be based on the summation of spectral lines values. The minimum number of lines to be taken into account is related to windowing function used for time block filtering. Up to 8 different orders may be extracted per channels. Order selection may be different from one channel to another.
Setting Constant Band Tracking Parameters
a/ Order Amplitude Extraction
Order amplitude extraction from FFT spectra is highly dependent on FFT speed itself. High resolution in FFT setting (very small delta f) will result in long trigger blocks and consequently slow FFT refreshes. Fast run or run down conditions (quickly changing vibration signature) may therefore be incompatible with slow FFT calculations. One way to avoid this problem may be to reduce Spectrum resolution to an acceptable value and add an Overlap (see picture 1) in FFT calculation.
The number of averages is also a parameter to look after as too many averages may smooth run up/down vibration signature. Contrarily too few averages may result in a noisy looking order amplitude curve.
Picture 1: Overlap setting
b/ Frequency bandwidth definition
Frequency band on which order amplitude may be extracted is to be defined by user for each channel (see picture 2). Too wide of a frequency band definition may lead to measurement errors, as harmonics from rotation speed may be very close at low speed. For instance at 1000 RPM, Order 1 will be at 16.6Hz, Order 2 at 33.2Hz, defining a frequency band for energy summation of 50Hz for instance for order 1 will result in integrating Order 1 and Order 2 in this case. More generally speaking the amplitude value of Order 1 calculated with Constant Band Tracking technique may often be overestimated during low speed analysis process.
Picture 2: frequency bandwidth definition
Minimum frequency bandwidth available
Minimum band available is directly related to weighting window type used in FFT calculation.
Due to window shape, energy of a pure tone sine wave for instance may be split on 3 or more spectral lines. Consequently, a minimum frequency band will be proposed in the setting window.
Example of Hanning window:
From the curve shown in Picture 3, you can see that applying Hanning weighting window on a pure tone sine wave will result in energy spread between the 2 side spectral lines (-1 and +1 on Picture 3) of sine frequency. Energy on the next spectral lines (-2 and +2 on Picture 3) will be reduced to 0 amplitude.
Picture 3: Hanning weighting window
c/ Phase calculation in Constant Band Tracking
In order to extract precise phase information from Constant Band Tracking, measurement have to be synchronized with rotational speed. Acquisitions of FFT blocks (trigger block) will need to be synchronized with Tach pulses in order to guaranty exact start condition in time (see Picture 4).
Picture 4: Trigger setup for CBT phase
Increase of phase precision with averaging domain.
Provided the FFT trigger condition is set to Tach pulses, averaging domain be can be set to Time. This will activate Time Shift Resampling (see User Note: S015-081-1 Time shift resampling) in time domain and therefore increasing phase accuracy of trigger block by a factor of 16.(see Picture 5)
Picture 5: Time domain averaging setting
Similarly, to guaranty that core information of Trigger Blocks (and therefore phase information) are not filtered out by weighting window, it is recommended to center time Trigger Blocks by shifting them half a block. This is made possible through the 'Start Delay' feature by adjusting it to a negative value of half the size of a trigger block (equivalent to 1/[2*"delta"f], where "delat"f is the spectral resolution). (see picture 6)
Picture 6: Trigger delay setting in CBT